Клеточные автоматы
Для нашей окончательной архитектуры мы собираемся использовать совершенно другой подход. Все агенты, которые мы создавали до сих пор, были «нисходящими» . Центральный, интеллектуальный агент принимает решения и выполняет планы. Но что, если мы перевернем это с ног на голову?
Вдохновленная сложными природными системами архитектура клеточных автоматов использует огромное количество простых децентрализованных агентов, работающих в сети.
Единого контроллера нет. Вместо этого, разумное общее поведение достигается за счет многократного применения простых локальных правил.
В крупномасштабной системе искусственного интеллекта это узкоспециализированный, но невероятно мощный подход для пространственного мышления, моделирования и оптимизации.
Представьте себе планирование логистики, моделирование заболеваний или моделирование роста городов. Это превращает само проблемное пространство в «вычислительную структуру», которая решает задачи посредством волнообразного распространения информации.
Это может быть очень сложно, но давайте попробуем разобраться, как это работает?
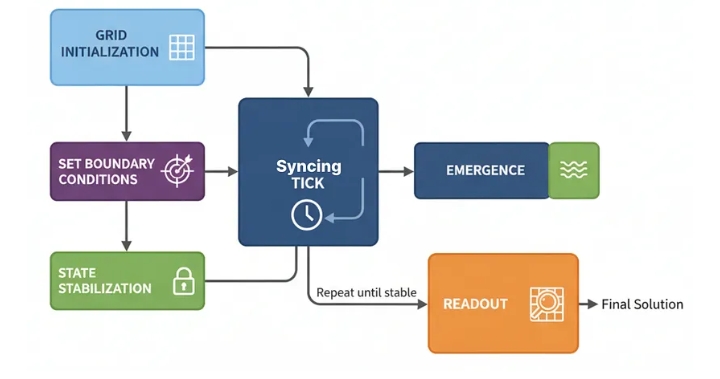
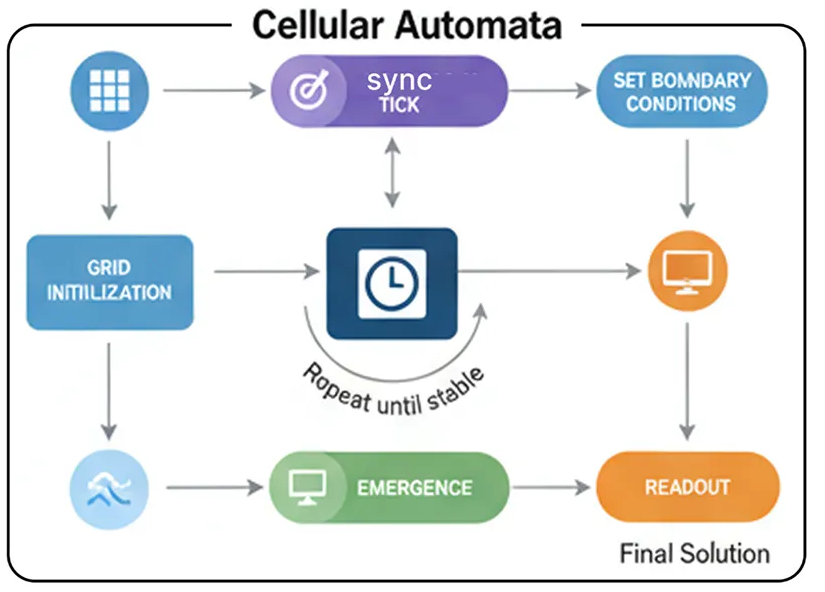
Клеточные автоматы (созданы)
Фарид Хан
)
Инициализация сетки: Создается сетка из «ячеек-агентов», каждая из которых имеет простой тип (например, OBSTACLE, EMPTY) и состояние (например, значение).
Установка граничных условий: Целевой ячейке присваивается специальное состояние для начала вычислений (например, ее значение устанавливается равным 0).
Синхронный тик: В каждом «тике» каждая клетка одновременно вычисляет свое следующее состояние, основываясь только на текущем состоянии своих непосредственных соседей.
Возникновение: По мере работы системы информация распространяется по сетке подобно волне, создавая градиенты и пути.
Стабилизация состояния: система работает до тех пор, пока изменения в сети не прекратятся, то есть вычисления не будут завершены.
Считывание данных: Решение считывается непосредственно из конечного состояния сетки.
В основе этой системы лежат CellAgentи WarehouseGrid. У CellAgentимеется одно простое правило: мое новое значение равно 1 + the minimum value of my non-obstacle neighbors.
10:40:59
class CellAgent :
"""Единственный агент в нашей сетке. Его единственная задача — обновлять свое значение на основе соседей."""
def __init__ ( self, cell_type: str ):
self. type = cell_type # 'EMPTY', 'OBSTACLE', 'PACKING_STATION', etc.
self.pathfinding_value = float ( 'inf' )
def update_value ( self, neighbors: List [ 'CellAgent' ] ):
"""Основное локальное правило."""
if self. type == 'OBSTACLE' : return float ( 'inf' )
min_neighbor_value = min ([n.pathfinding_value for n in neighbors])
return min (self.pathfinding_value, min_neighbor_value + 1 )
class WarehouseGrid :
def __init__ ( self, layout ):
self.h, self.w = len (layout), len (layout[ 0 ])
self.grid = np.array([[self._cell(ch) for ch in row] for row in layout], dtype= object )
def _cell ( self, ch ):
return CellAgent( 'EMPTY' ) if ch== ' ' else \
CellAgent( 'OBSTACLE' ) if ch== '#' else \
CellAgent( 'PACKING_STATION' ) if ch== 'P' else CellAgent( 'ПОЛКА' ,item=ch)
def neighbors ( self,r,c ):
return [self.grid[nr,nc] for dr,dc in [( 0 , 1 ),( 0 ,- 1 ),( 1 , 0 ),(- 1 , 0 )]
if 0 <=(nr:=r+dr)<self.h and 0 <=(nc:=c+dc)<self.w]
def tick ( self ):
vals = np.array([[cell.update_value(self.neighbors(r,c))
for c,cell in enumerate (row)] for r,row in enumerate (self.grid)])
changed= False
for r,row in enumerate (self.grid):
for c,cell in enumerate (row):
if cell.pathfinding_value!=vals[r,c]: changed= True
cell.pathfinding_value=vals[r,c]
return changed
def visualize ( self,show= False ):
t=Table(show_header= False )
[t.add_column() for _ in range (self.w)]
sy={ 'EMPTY' : '·' , 'OBSTACLE' : '█' , 'PACKING_STATION' : 'P' }
for r in range (self.h):
row=[]
for c in range (self.w):
cell,val=self.grid[r,c],self.grid[r,c].pathfinding_value
if show and val!= float ( 'inf' ):
col= 255 -(val* 5 )% 255
row.append( f"[rgb( {col} , {col} , {col} )] { int (val):^ 3 } [/]" )
else :
row.append(sy.get(cell. type ,cell.item))
t.add_row(*row)
console. print (t)

Сотовый подход (создан)
Теперь мы можем реализовать высокоуровневую логику, которая использует эту вычислительную структуру для поиска пути. Функция propagate_path_waveустанавливает целевое значение (например, упаковочную станцию) равным 0, а затем позволяет сетке работать tickдо тех пор, пока значения пути не распределятся по всему складу.
def propagate_path_wave ( grid: WarehouseGrid, target_pos: Tuple [ int , int ] ):
"""Сбрасывает и затем запускает симуляцию до тех пор, пока значения поиска пути не стабилизируются."""
# Сбрасываем все значения поиска пути до бесконечности
for cell in grid.grid.flatten(): cell.pathfinding_value = float ( 'inf' )
# Устанавливаем значение цели равным 0, чтобы начать волну
grid.grid[target_pos].pathfinding_value = 0
while grid.tick(): # Продолжаем тикать, пока сетка не стабилизируется
passДавайте создадим схему расположения товаров на складе и укажем ей найти путь от товара «А» до упаковочной станции «P».
warehouse_layout = [
"#######" ,
"#A #" ,
"# ### #" ,
"# # #" ,
"# # # #" ,
"# P #" ,
"#######" ,
]
grid = WarehouseGrid(warehouse_layout)
packing_station_pos = grid.item_locations[ 'P' ]
propagate_path_wave(grid, packing_station_pos)
Вся магия в том, что мы не рассчитывали путь. Сетка вычислила кратчайший путь от каждого квадрата до упаковочной станции одновременно. В результате получился красивый градиент, обтекающий препятствия.

Числа обозначают расстояние до точки «P». Чтобы найти путь от точки «A», агенту достаточно начать движение из её местоположения (значение 8) и всегда двигаться к соседней точке с наименьшим числом (7, затем 6 и т. д.). Он просто следует по уклону вниз.
Шаг 1: Выполните пункт «А»
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓
┃ 🌊 Расчет траектории движения от упаковочной станции...
┃ 🚚 Найден путь для товара А. Движение вдоль градиента...
┃ Путь: (3, 0) -> (3, 1) -> (3, 2) -> (4, 2) -> (5, 2) -> (5, 3)
┃ ✅ Товар «А» перемещен на упаковочную станцию.
┗━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┛
Шаг 2: Выполните пункт 'B'
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓
┃ 🌊 Вычисление траектории движения от упаковочной станции...
┃ 🚚 Найден путь для предмета B. Движение вдоль градиента...
┃ Путь: (4, 5) -> (4, 4) -> (4, 3) -> (5, 3)
┃ ✅ Товар 'B' перемещен на упаковочную станцию.
┗━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┛
Заказ на товары A и B успешно выполнен. Товар А был извлечен с полки в точке с координатами (3, 0) и перемещен по 6-шаговому маршруту к упаковочной станции. Затем товар В был извлечен из точки (4, 5) и перемещен по 4-шаговому маршруту к тому же месту назначения. Пол склада теперь свободен и готов к приему следующего заказа.
Наш агент начинает думать, это совершенно другой способ мышления агентов. Рассуждения распределены по всей системе.
Чтобы это формализовать, наш магистр права, выступающий в роли судьи, не может оценивать «решение», но он может оценивать сам процесс .
class EmergentBehaviorEvaluation (BaseModel):
optimality_score: int = Field (description= "Оценка от 1 до 10, гарантирующая ли эмергентный процесс нахождение оптимального решения." )
robustness_score: int = Field (description= "Оценка от 1 до 10, определяющая способность системы адаптироваться к изменениям в окружающей среде." )
justification: str = Field (description= "Краткое обоснование оценок." )
По результатам оценки, этот процесс заслуживает высшей оценки за свою надежность.
--- Оценка процесса клеточного автомата ---
{
'optimality_score' : 7 ,
'robustness_score' : 8 ,
'justification' : "Процесс системы является одновременно оптимальным и устойчивым. Метод распространения волн представляет собой разновидность поиска в ширину, что гарантирует кратчайший путь. Кроме того, решение возникает из локальных правил, то есть, если добавляется препятствие, повторный запуск моделирования автоматически найдет новый оптимальный путь без каких-либо изменений в основном алгоритме."
}
Хотя это очень специализированная область…
Клеточные автоматы могут быть чрезвычайно эффективны для решения определенных задач, например, когда нам необходимо предложить параллельный и адаптируемый способ обработки сложных пространственных задач.

